Airy Disk
Definitions
Aperture
- How much light is being passed through a lens
- Controlled by closing up or opening up the fans in the lens
- Measured in f stops
- Lower f stop means more light and thinner focal plane
- Higher f stop means less light and wider focal plane
Diffraction
- Light bending and spreading out due to obstacles
- More apparent as you go a higher f stop
Airy Disk
- Light pattern that occurs due to diffraction of light through a circular aperture (lens)
- Pattern is a central bright spot with rings propegating around it
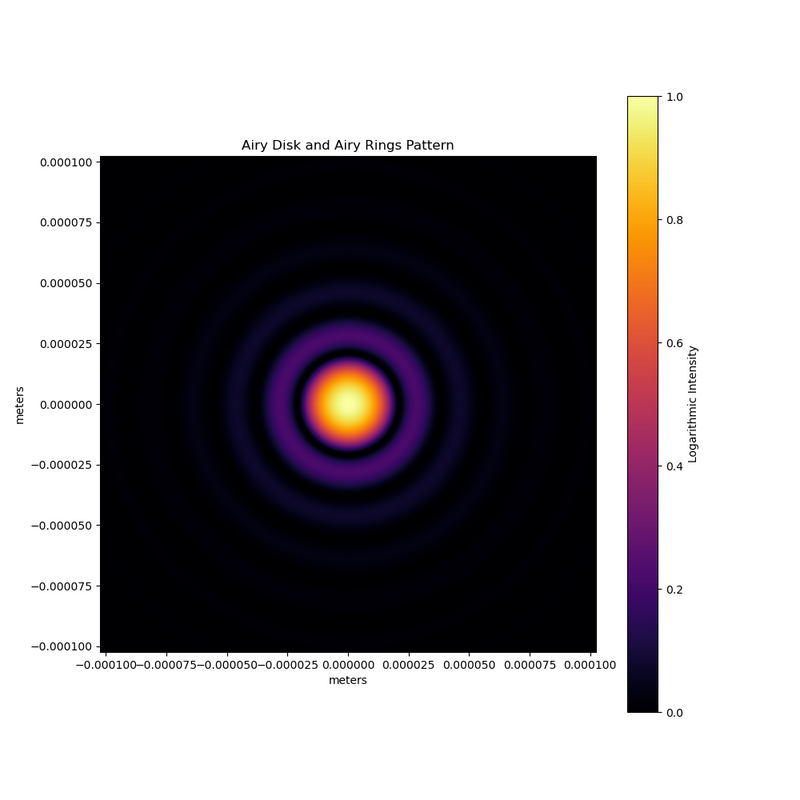
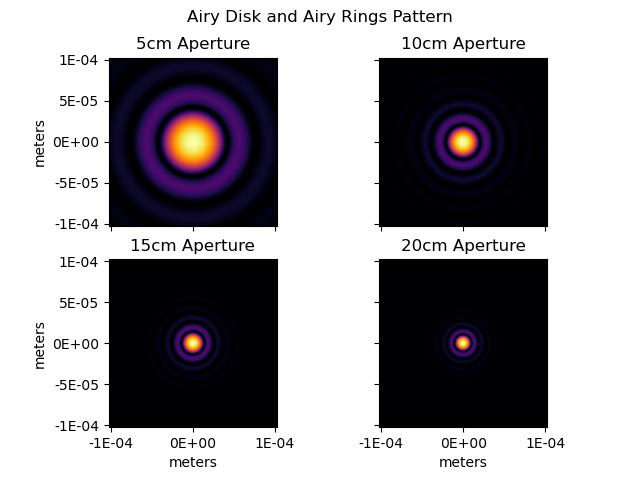
- The rings are called Airy Rings
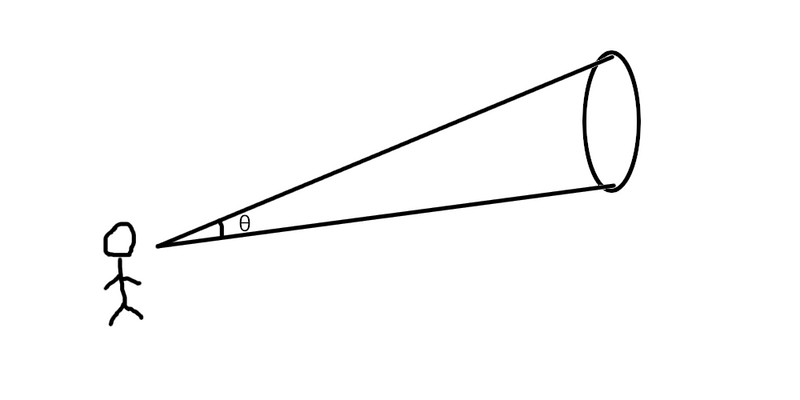
Angular Diameter
- Value used to describe how large a sphere/circle is from a given point of view
Application
Rayleigh Criterion
- Funamental principle used to determine the resolution limit of an optical system
- It calculates the the minimum angular distance between two points of light sources that allows them to be distinctly identified as separate objects.
- Essentially as long as the airy disk from one source does not coincide with the other light sources airy disk the object can theoretically be distinctly identified

- \(\theta\) is angular diameter in radians
- \(\lambda\) is the wavelength of the light
- d is the diameter of the aperture
- Assumes aperture is perfectly circular
- Assumes only one wavelength range.
import math
import numpy as np
# Parameters
# Wavelength in meters
wavelength = 550e-9
# Aperture diameter in meters
D = 0.1
ang_dist_rad = 1.22 * wavelength/D
ang_dist_deg = ang_dist_rad * (180 / math.pi)
ang_dist_arc = ang_dist_rad * (180 * 3600 / math.pi)
print(ang_dist_rad)
# 6.71e-06
print(ang_dist_deg)
# 0.0003844546805327824
print(ang_dist_arc)
# 1.3840368499180167
- Calculation above means that for the wavelength of 550nm (green) with an apecture of 10cm we can theoretically distinguish two light sources that are 1.384 arcseconds away from eachother
Appendix
# Generate Airy Disk and Rings
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import jn
# Parameters
# Wavelength in meters
wavelength = 550e-9
# Aperture diameter in meters
D = 0.1
# Pixel size in meters
pixel_size = 2e-7
# Size of the simulation grid
size = 1024
# Create a grid
x = np.linspace(-size/2, size/2, size) * pixel_size
y = np.linspace(-size/2, size/2, size) * pixel_size
X, Y = np.meshgrid(x, y)
R = np.sqrt(X**2 + Y**2)
# Calculate wavenumber
k = 2 * np.pi / wavelength
# Airy pattern calculation
alpha = k * D * R / (2 * np.pi)
intensity = (2 * jn(1, alpha) / alpha)**2
# Scale for better visualisation
intensity_log = np.log10(intensity + 1e-2)
# Normalize the intensity between 0 and 1
intensity_log -= np.min(intensity_log)
intensity_log /= np.max(intensity_log)
# Plot the Airy disk and rings
plt.figure(figsize=(10, 10))
plt.imshow(intensity_log,
extent=[x.min(), x.max(), y.min(), y.max()],
cmap='inferno',
origin='lower')
plt.colorbar(label='Logarithmic Intensity')
plt.title('Airy Disk and Airy Rings Pattern')
plt.xlabel('meters')
plt.ylabel('meters')
plt.savefig("airy_disk_ring")
plt.show()
Written on August 12, 2024