Definitions

Camera Calibration

• Process of determining the parameters of a lens+camera that allows you to accurately compute measurements and positions.
• Useful for
  • measuring a size of an object from an image in the world unit
  • Determining the location of the camera in the scene
  • Stiching images together
  • Un/distort an image

Extrinsic Matrix

• Represents the position and orientation of the camera in respect to the coordinate system it’s in
• Includes rotation and translation values

• \(R\) - 3x3 rotation matrix

• Rotation matrix multiplication order matters

• \(T\) - 3x1 position of the camera

Intrinsic Matrix

• Represents the internal parameters of the camera
• Includes focal length, principal point and skew coefficient

• Focal length (\(f_x, f_y\)) - Scale of the image measured in pixels.
  • \(F\) - focal length of lens in mm
  • \(p_x, p_y\) - size of pixel in world units

• Principal point (\(c_x, c_y\)) - location on the camera’s image in pixels where the lens’s optical axis (the line going straight through the center of the lens) would hit the image sensor

• Skew coefficient (\(s\)) - measure of how much the image axes (x and y) are not perfectly perpendicular to each other.

Radial Distortion

• Distortion that occurs from light bending near the edges of a lens which make straight lines appear warped

• \(x,y\) - undistored pixel location in the normalized image coordinate space.
• \(k_1, k_2, k_3\) - radial distortion coefficients of the lens

Tangential Distortion

• Distortion that occurs when the lens and imgage sensor are not parallel

• \(x,y\) - undistored pixel location in the normalized image coordinate space.
• \(p_1, p_2\) - tangential distortion coefficients of the lens

Example

Radial Positive

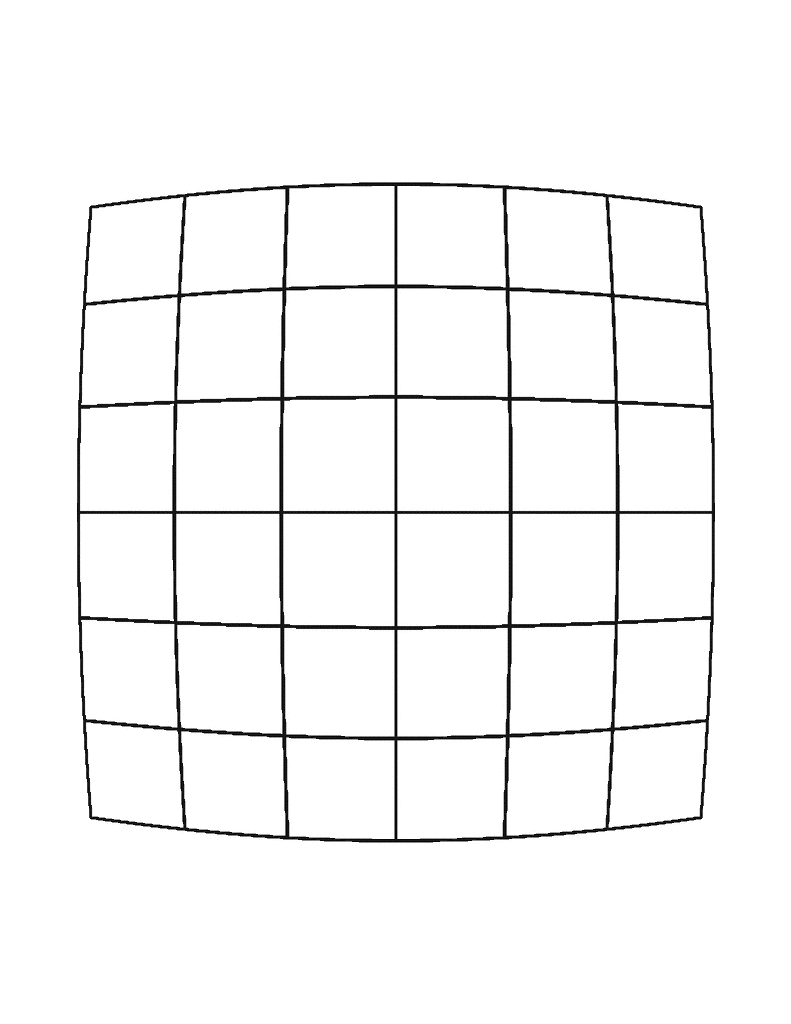
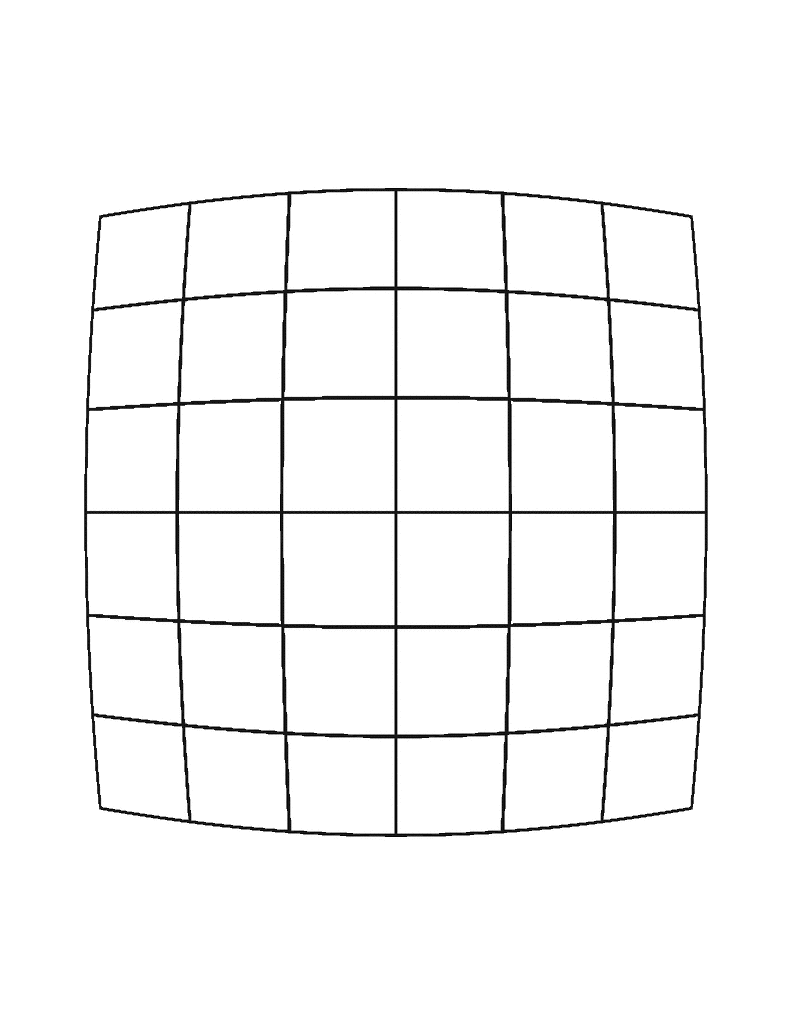
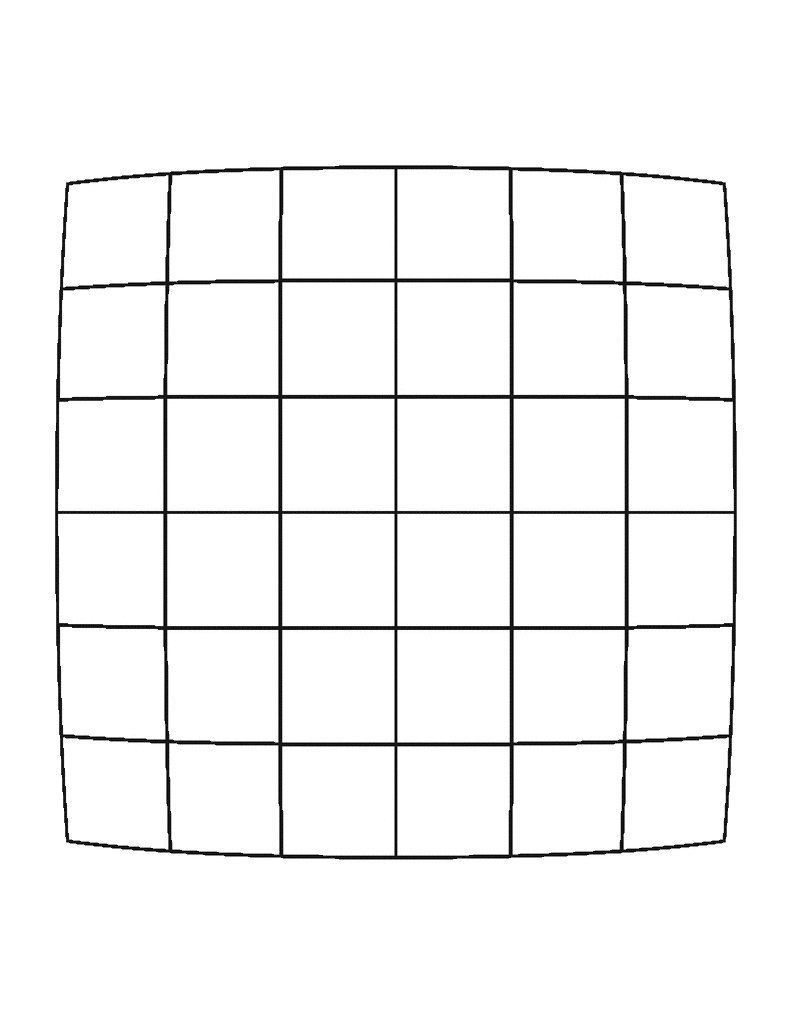
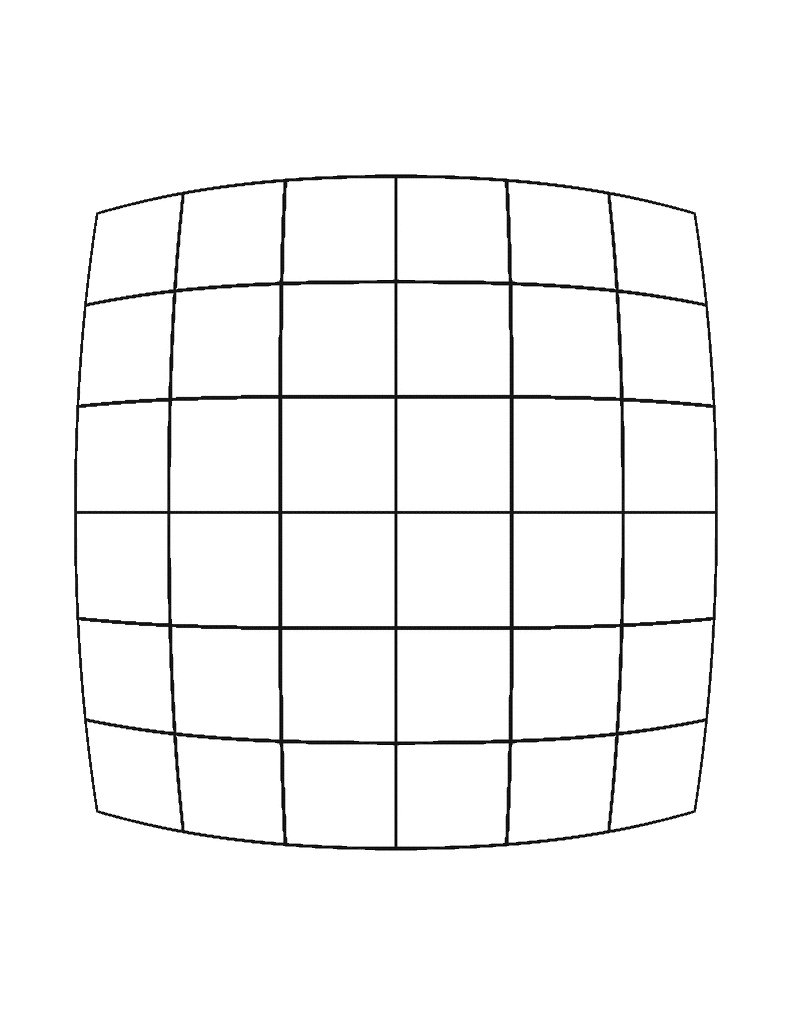
Radial Negative

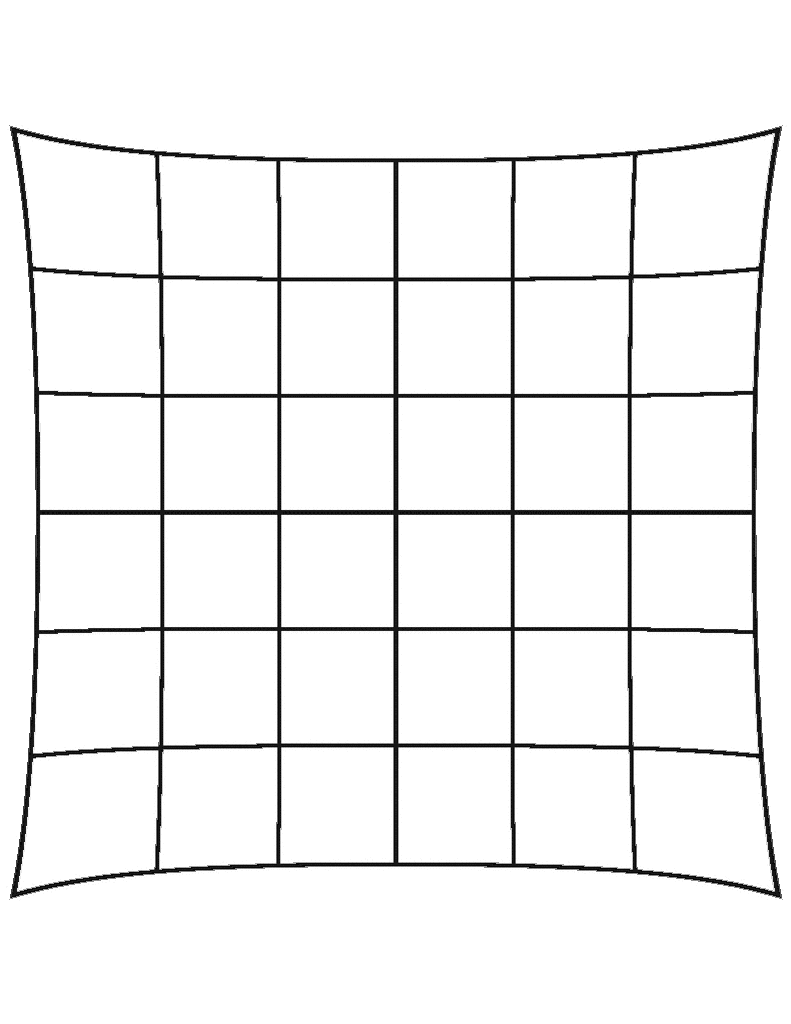
Tangential Positive

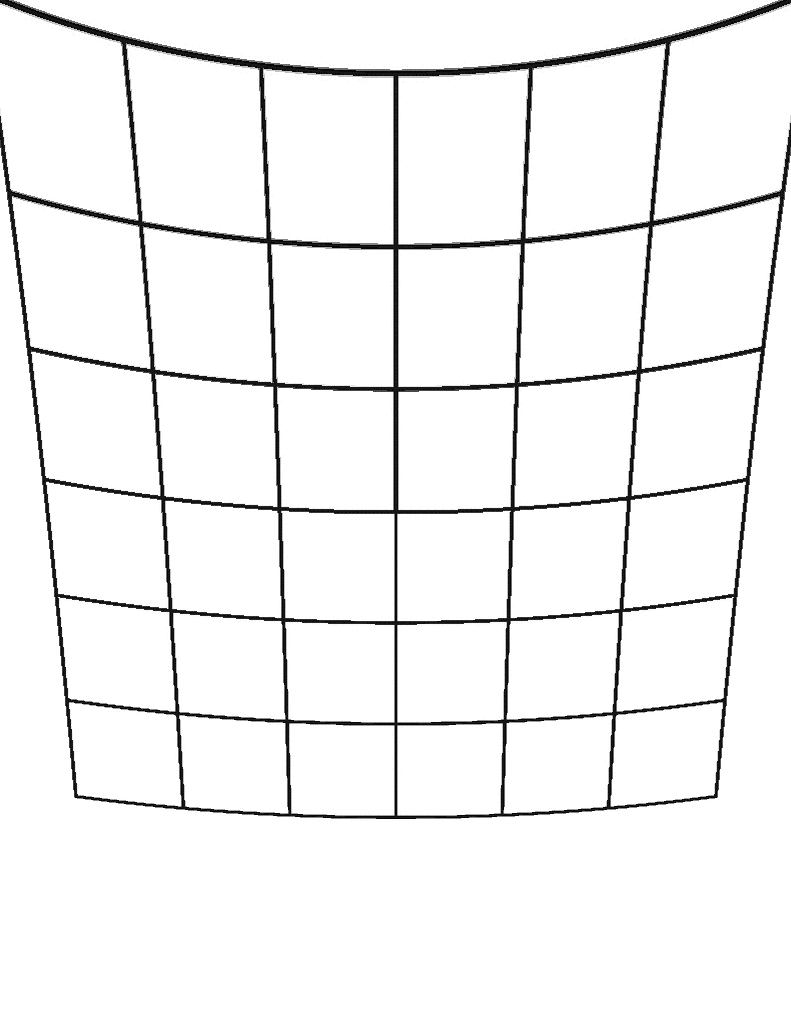
Tangential Negative

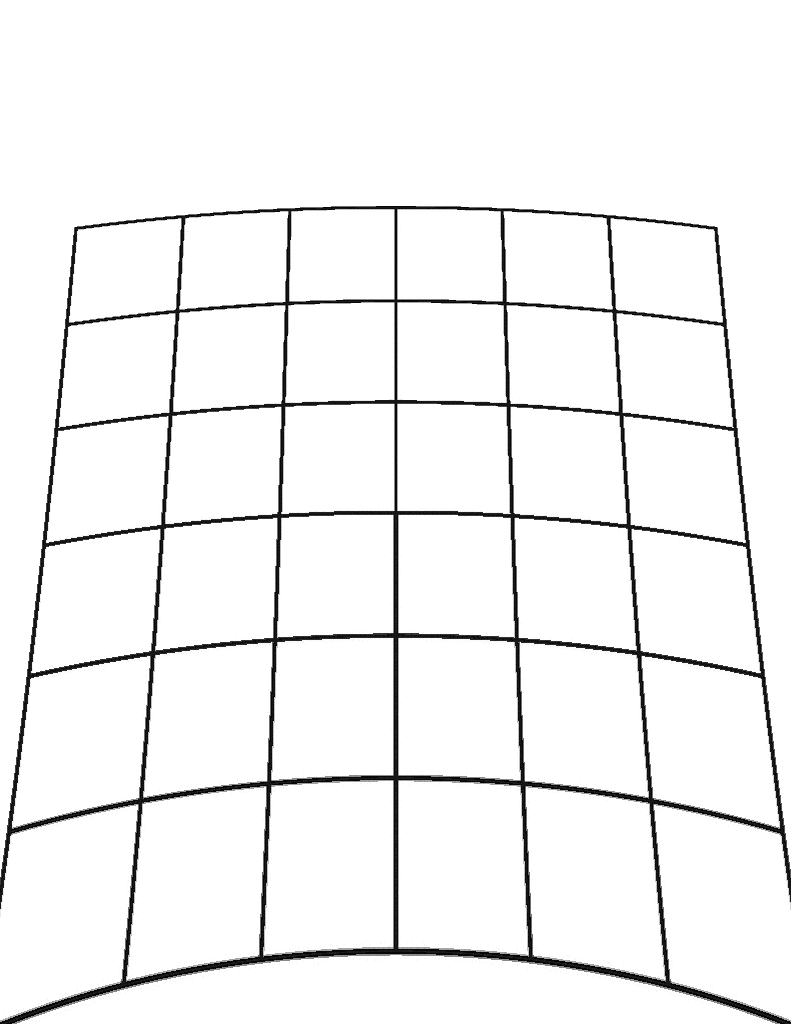
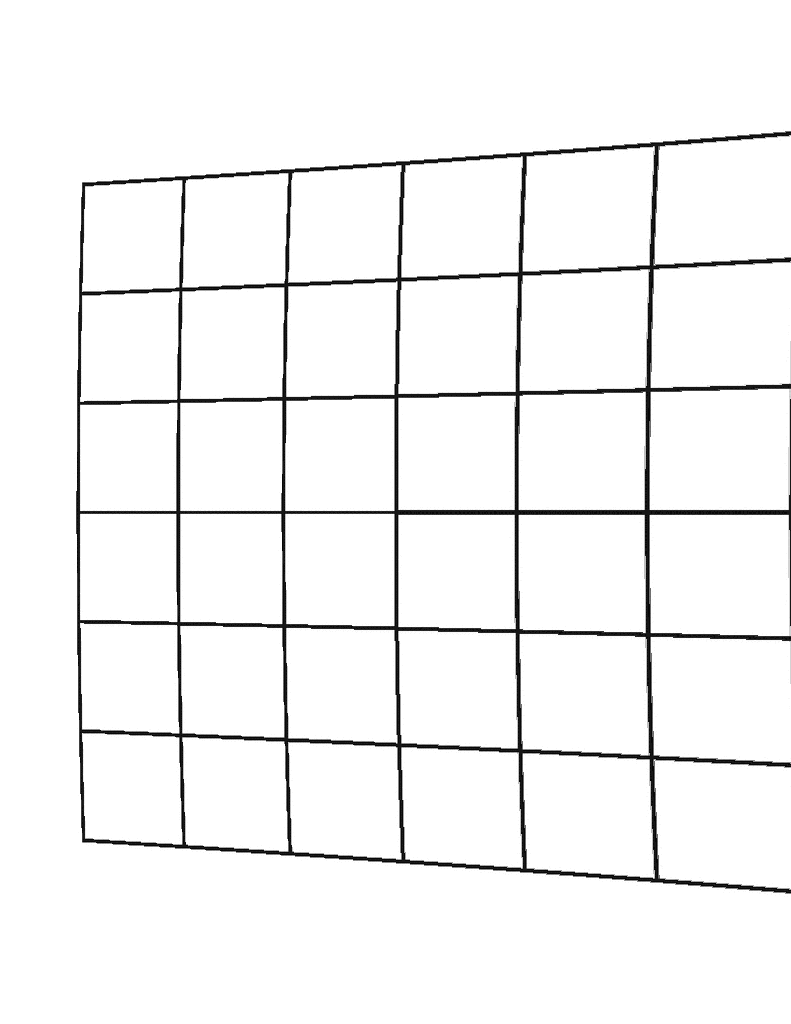
Calculating Parameters

• Using OpenCV you can calculate the intrinsic + extrinsic matrix and the distortion coefficients
• for more information
• tldr
  • Use 10 images or so with some known points in 3D space (object points) and corresponding 2D space (image points)
  • Feed images into cv.calibrateCamera

import numpy as np
import cv2 as cv
import glob

# termination criteria
criteria = (cv.TERM_CRITERIA_EPS + cv.TERM_CRITERIA_MAX_ITER, 
            30,
            0.001)
 
# prepare object points, like (0,0,0), (1,0,0), ....,(6,5,0)
objp = np.zeros((6*7,3), np.float32)
objp[:,:2] = np.mgrid[0:7,0:6].T.reshape(-1,2)
 
# Arrays to store object points and image points 
# from all the images.
objpoints = [] # 3d point in real world space
imgpoints = [] # 2d points in image plane.
 
images = glob.glob('*.jpg')
 
for fname in images:
    img = cv.imread(fname)
    gray = cv.cvtColor(img, cv.COLOR_BGR2GRAY)
 
    # Find the chess board corners
    ret, corners = cv.findChessboardCorners(gray, (7,6), None)
 
    # If found, add object points, image points (
    # after refining them)
    if ret == True:
        objpoints.append(objp)
 
        corners2 = cv.cornerSubPix(gray,corners, 
                                   (11,11), 
                                   (-1,-1), 
                                   criteria)
        imgpoints.append(corners2)

# calculate the camera/intrinsic matrix, 
# distortion coefficients, 
# rotation and translation vectors
result = cv.calibrateCamera(objpoints, 
                            imgpoints, 
                            gray.shape[::-1], 
                            None, 
                            None)
ret, int_mtx, dist, rvecs, tvecs = result

Intrinsic Matrix

Radial Distortion Coefficients

Tangential Distortion Coefficients

img = cv.imread('left12.jpg')

# undistort
dst = cv.undistort(img, mtx, dist)
 
# save the image
cv.imwrite('calibresult.png', dst)

FAQ

Why isn't the principal point always 0,0?

• In an ideal world with no manufacturing issues or lens alignment issues the principal point could be 0,0. But we do not live in an ideal world.
• Small imperfections and tolerances are everywhere and even the slightest shift can result in a non 0,0 principal point.

Why isn't the skewer coefficient always 0,0?

• Same reason as the principal point.

Appendix

# Distort an image based on the distortion coeffs
import numpy as np

def distort_point(x, y, width, height, r_coeffs, t_coeffs):
    k1, k2 = r_coeffs[:2]
    p1, p2 = t_coeffs[:2]
    
    x_c = width/2
    y_c = height/2

    x = (x - x_c) / x_c
    y = (y - y_c) / y_c

    # Radial distortion
    r2 = x**2 + y**2
    rad_dist = 1 + k1 * r2 + k2 * r2**2
    
    # Tangential distortion
    tang_dist_x = 2 * p1 * x * y + p2 * (r2 + 2 * x**2)
    tang_dist_y = (p1 * (r2 + 2 * y**2) + 2 * p2 * x * y)

    x_distorted = x * rad_dist + tang_dist_x
    y_distorted = y * rad_dist + tang_dist_y
    
    x_distorted = x_distorted * x_c + x_c
    y_distorted = y_distorted * y_c + y_c

    return x_distorted, y_distorted

def distort_image(image, r_coeffs, t_coeffs):
    """ Distort an entire image. """
    h, w = image.shape[:2]
    d_image = np.full_like(image, 255)

    for y in range(h):
        for x in range(w):
            x_d, y_d = distort_point(x, y, 
                        w, h, r_coeffs, t_coeffs)
            if 0 <= int(x_d) < w and 0 <= int(y_d) < h:
                d_image[y, x] = image[int(y_d), int(x_d)]

    return d_image